 It’s All a Matter of Time: Interval Timing and Competition for Stimulus Control
It’s All a Matter of Time: Interval Timing and Competition for Stimulus Control
Neil McMillan
Department of Psychology, University of Alberta
Department of Psychology, University of Western Ontario
Marcia L. Spetch
Department of Psychology, University of Alberta
Christopher B. Sturdy
Department of Psychology and Neuroscience
and Mental Health Institute, University of Alberta
William A. Roberts
Department of Psychology, University of Western Ontario
Reading Options:
Continue reading below, or:
Read/Download PDF | Add to Endnote
Interval timing has been widely studied in humans and animals across a variety of different timescales. However, the majority of the literature in this topic has carried the implicit assumption that a mental or neural “clock” receives input and directs output separately from other learning processes. Here we present a review of interval timing as it relates to stimulus control and discuss the role of learning and attention in timing in the context of different experimental procedures. We show that time competes for control over behavior with other processes and suggest that when moving forward with theories of interval timing and general learning mechanisms, the two ought to be integrated.
Keywords: interval timing, reversal learning, inhibition, cue competition,
peak procedure, pigeons
Author Note: Neil McMillan, Department of Psychology, University of Alberta, 11455 Saskatchewan Drive, Edmonton, Alberta, T6G 2E9, Canada.
Correspondence concerning this article should be addressed to Neil McMillan at neil.mcmill@gmail.com.
Acknowledgments: This research was supported by Natural Sciences and Engineering Research Council of Canada Discovery Grants to M. L. Spetch, C. B. Sturdy, and W. A. Roberts. Parts of this document previously composed thesis dissertation chapters by N. McMillan.
Many modern humans explicitly experience time through its cultural constructs: We check our watches to determine if we have to leave for a meeting, we give directions based on how many minutes one should walk down a particular street before turning, and we hit snooze on our alarm clocks and dread the 10-min countdown to when we must roll out of bed. However, these daily experiences represent a sliver of how much time affects our lives, and our reliance on language-based social constructs such as “seconds” and “hours” belies an impressive, evolutionarily inbuilt system of timers that constantly govern behavior and cognition. It is not until we observe the breadth and accuracy of timing in nonhuman animal species that we can truly grasp how important these systems are.
Interval timing is the timing of stimulus durations of seconds to minutes to hours, and has been of great interest to researchers in a wide variety of behavioral and cognitive neuroscience disciplines (Buhusi & Meck, 2005). Whereas circadian timing is coordinated by the suprachiasmatic nucleus and is concerned with regulating daily (24-hr) patterns such as the sleep cycle and feeding, and millisecond timing is a largely cerebellar process that assists mostly in motor coordination, interval timing is possibly distributed over a complex striato-thalamo-cortical pathway and is useful over a huge range of timescales and for different purposes. Interval timing is pervasive across species (Richelle & Lejeune, 1980) and wherever the environment features temporal regularities (Macar & Vidal, 2009); is necessary for survival in dynamic environments (Antle & Silver, 2009); and is frequently considered in the literature to be an obligatory, automatic process (e.g., Roberts, Coughlin, & Roberts, 2000; J. E. Sutton & Roberts, 1998; Tse & Penney, 2006; Wynne & Staddon, 1988). All events occur at some place within some time, so it is perhaps not surprising that animals seem to rely heavily upon timing to best predict the occurrence of salient events.
Compared to spatial and numerical cognition, temporal cognition is arguably less well represented in the literature and in lab groups across the world, and tends to exist in isolation rather than being connected to other fields in perception and cognition. This may speak to the ineffable nature of time: Whereas space and number are at least superficially straightforward representations of the relationship between physical objects, time can be an extremely difficult construct to define. Time is not perceived as energy emanating from the environment, as all other stimulus domains inevitably are; instead, timing is an internal process derived partially from the change in those other stimuli, and indeed can be perceived even while incoming sensory information is blocked. Likewise, it has proven difficult to narrow down individual brain regions responsible for interval timing beyond a complicated network of interconnected areas (Merchant, Harrison, & Meck, 2013). Nonetheless, a number of recent reviews have been aimed at summarizing, for example, how time is ubiquitously important to animals (and thus well represented across theories of behavior; Marshall & Kirkpatrick, 2015), encompasses a breadth of integrative research (Balci, 2015), and can be connected with multiple areas of cognition despite the subjectivity of its experience (Matthews & Meck, 2016). We do not rehash these reviews of the concepts and processes of time; instead, here we focus on how time competes with other dimensions more traditionally perceived as “stimuli” for control over behavior, with the overarching goal of presenting interval time in the framework of behavior as not just a cognitive dimension but a stimulus in and of itself.
Given the insular nature of timing research, one of the greatest paradoxes in the literature is that many studies include time as a parameter in some form. Interval time plays a defining role in contiguity, memory, and any calculation of rate, so in some ways it might be one of the most studied elements of learning and cognition. On the other hand, most of these studies are unconcerned with how time is actually processed, or variations in time are assumed to correspond to straightforward changes in the process being studied without specific input from a “clock” process (e.g., longer durations of or between sample and choice affecting short-term memory; Roberts & Grant, 1974, 1976, 1978). Because studying interval timing tends to be divorced from studying other learning processes, interactions that the two systems might have are largely overlooked. Although time is relevant in many experimental procedures, most studies explicitly examining interval timing in animals use one of two procedures: the temporal bisection task or the peak procedure. We briefly review those procedures, as well as current understanding of the mechanisms of interval timing, before returning to the question of integration of interval timing with other processes.
In the temporal bisection task (Church & Deluty, 1977), generally an animal is provided two response alternatives, one of which is correct after a stimulus presentation that is “short” (e.g., a 1-s tone burst) and the other correct after a “long” stimulus duration (e.g., a 4-s tone burst). Trained durations and task specifics vary across studies, but the main findings include that animals are able to discriminate between durations and respond appropriately; further, under testing conditions with untrained intermediate stimulus durations, animals tend to bisect functions at the geometric rather than the arithmetic mean between the anchor durations (e.g., at 2 s rather than 2.5 s, with the previous examples; see Church & Deluty, 1977; Meck, 1983).
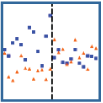
In the main alternative to temporal bisection for studying interval time, the peak procedure (Catania, 1970; S. Roberts, 1981), subjects are trained on a fixed-interval (FI) reinforcement schedule in which, repeatedly, the first response after a fixed period is rewarded. Then unreinforced peak probe trials are introduced, typically of double or triple the length of the contingent FI. Thus, rather than making a discrete response to different intervals, animals are asked to “produce” the interval. Curves showing rate of response over the course of peak trials typically show a normal distribution of responses over the interval, with the peak at or around the expected point of food reinforcement (S. Roberts, 1981; see Figure 1A for an example). Although individual trials tend to involve break-run-break periods of all-or-nothing responding (Cheng & Westwood, 1993; Gibbon & Church, 1990; see Figure 1B for an example), averaging trials that start and stop at different times yields smooth Gaussian-like curves. The width of the curve around the peak, the response duration spread, represents noise in the representation of time and exhibits scalar properties (Gibbon, 1977). Peak-trial responding is thus consistent with Weber’s Law, wherein the degree of error (i.e., response spread) is proportional to the mean of the produced interval. Scalar variability is one of the primary findings in the peak procedure that all models of timing must account for.
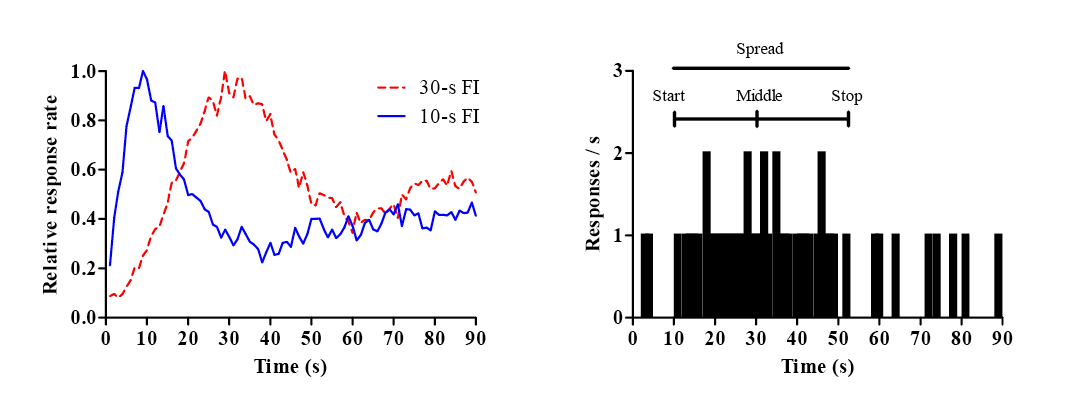
Figure 1. (A; Left Panel) Example of a typical peak-time curve, generated from previous data in our lab by averaging data gathered on empty peak trials for birds trained on 10-s or 30-s FIs. Response data relativized to a maximum of one response per second. (B; Right Panel) Example of responding on a single empty peak interval trial from a bird trained with a 30-s FI in a previous study in our lab. This illustrates the characteristic break-run-break function in responding, which when averaged across trials and subjects produces a graded response curve similar to that in Panel A. Start time reflects the shift from low to high states of responding, and stop time the change from high to low states of responding; middle time is presumed to reflect the expected time of reinforcement.
What’s Time Without a Clock? Models of Interval Timing
Many theories have been developed to explain the data obtained with the peak procedure; there are conspicuously about as many theories of timing as there are labs focused on studying the construct. In the most cited of these theories, scalar expectancy theory (typically used interchangeably with the later scalar timing theory), the internal clock consists of a neural pacemaker that emits pulses, a switch that closes when a signal indicates the beginning of an interval to be timed, and an accumulator that sums pulses from the pacemaker (Gibbon & Church, 1984, 1990; Gibbon, Church, & Meck, 1984). The number of pulses accumulated at the moment of reinforcement on training trials is stored in reference memory, and these numbers are randomly retrieved as criterion values on subsequent trials. A comparator mechanism continually compares accumulated pulses in working memory with the criterion value and initiates responding when the difference between the accumulator and criterion drops below a threshold. Because the difference between the accumulator and criterion is recorded as an absolute value, the comparator also stops responding when the difference threshold is exceeded. Because the theory uses the same comparator process to start and stop responding, the symmetry of peak-time curves is predicted. Although scalar timing theory predates most modern knowledge of neuroscience, and it has been succeeded by other theories, it still has ardent supporters (e.g., see Wearden, 2016) and tends to be the model against which all others are judged.
In the most popular alternative theories of timing, behavioral judgments of time are more closely related to traditional associative processes. The behavioral theory of timing (Killeen & Fetterman, 1988) suggests that a pacemaker initiated at the beginning of an FI advances an animal through successive adjunctive behavioral states and that the behavioral state present at the moment of reinforcement will be conditioned to elicit responding. Because the pacemaker advances according to a Poisson process, this theory predicts the gradient of responding around the FI on peak timing probe trials. However, one of the issues facing the behavioral theory of timing is that there has been little success in showing these deterministic patterns of behavior during the temporal interval (Lejeune, Cornet, Ferreira, & Wearden, 1998). Machado (1997) offered a similar dynamic behavioral model based on real time, called the learning-to-time model, in which a stimulus that initiates an FI activates a series of behavioral states. Each state becomes associated to some extent with the reinforced operant response, but responding during nonreinforced states is weakened through extinction. Important to note, because time is based on the diffusion of activation across many states, this model does not experience the same problems as standard behavioral timing theory when faced with variable behavior as subjects time. The learning-to-time model has been applied recently to understanding how temporal generalization gradients can explain a wealth of behavioral data (de Carvalho, Machado, & Vasconcelos, 2016).
Contrary to models based on behavioral state-based clocks, trace-based clocks are assumed to measure time based on continuous neural traces. For example, in Staddon and Higa’s (1999) multiple-time-scale model, timing is based on the formation of associations between the reinforced response and the strength of a memory trace of a signal that began the interval to be timed. These traces of the starting signal decay, and traces with strengths near those of previously reinforced intervals will evoke more responding than those that are either stronger (shorter intervals) or weaker (longer intervals). In the conceptually similar spectral timing model (Grossberg & Schmajuk, 1989), different spectra of gated neurons are active at different times after the onset of a conditioned stimulus, providing a cascade of different timing signals, with the peaks in these traces becoming differentially associated with the unconditioned stimulus.
Finally, many recent theories of timing have focused on neural oscillators as the foundation of the clock process, such as the multiple-oscillator model (Church & Broadbent, 1990). Oscillating neurons fluctuate back and forth from –1 to 1 states sinusoidally, such as seen in the neurons (or neural networks) guiding heart rate, breathing rate, and circadian rhythms. Theories of timing involving oscillators generally suggest that the onset of the conditioned stimulus synchronizes the period of many oscillators, which then beat at different rates. At the time of reinforcement, the current set of states across the oscillators is stored, and this stored state serves as the measure of time. The striatal beat-frequency model (Matell & Meck, 2000, 2004) similarly suggests that timing results from detection of coincident oscillator states by spiny neurons in the striatum. Like trace models, oscillator clocks are biologically plausible because they make use of actual features of neural networks. Recent evidence has also suggested that animals have a nonlinear sensitivity to time, which is consistent with oscillator models (see Crystal, 2012, 2015). The striatal beat-frequency model, in particular, is attractive because of its combination of the biologically grounded beat frequency model (Miall, 1989) with principles from the well-studied scalar expectancy theory.
Many timing models presume the interval clock to be an internal neural process that is not affected by outside stimulation other than the initial CS (i.e., the cue to start) and the US (the cue to stop). Although these models thus tend to be variably successful at predicting results of relatively complex timing experiments (e.g., timing multiple stimuli simultaneously), they also tend to be silent on how time might be processed in competition with nontemporal processes. Typical models of timing do not generally include explicit parameters for signal characteristics (e.g., different modalities of stimuli to be timed), attention sharing, or reward value effects, and instead tend to assume that time is automatically processed by the internal clock. A wealth of literature has shown various effects of nontemporal aspects of stimulus presentation on the timing of intervals or gaps in intervals, with accuracy affected by stimulus modality (Meck, 1984; Roberts, Cheng, & Cohen, 1989), stimulus intensity (Wilkie, 1987), reward value (Galtress & Kirkpatrick, 2009, 2010; Ludvig, Balci, & Spetch, 2011), and filled versus empty intervals (Miki & Santi, 2005; Santi, Keough, Gagne, & Van Rooyen, 2007; Santi, Miki, Hornyak, & Eidse, 2005). Common theories of timing typically must be amended in a post hoc manner to account for attentional or stimulus dimension effects; for example, attentional models of timing in humans (Block & Zakay, 1996) explicitly create a gating mechanism representing attentional control, fluctuations in which lead to “loss” of accumulated pulses and a tendency to underestimate interval duration. More commonly, models of timing simply remain mute to nontemporal inputs.
Alternative theories of timing account for nontemporal effects on timing by omitting the clock process altogether. Ornstein (1969) suggested that timing is simply a deduction of elapsed duration by the amount of information processed: Shorter intervals naturally allow for less processing, whereas long intervals allow for a greater amount of processing. According to this theory, filled intervals and high-intensity stimuli are predicted to be timed as longer than empty intervals or low-intensity stimuli because more information processing occurs and thus time is perceived as subjectively longer; this effect is commonly observed in data (e.g., Santi et al., 2005; Wilkie, 1987), though “information processing” is left vaguely defined. Likewise, a number of more recent theories have attempted to fit clockless associational models (e.g., Arcediano & Miller, 2002; Dragoi, Staddon, Palmer, & Buhusi, 2003; Kirkpatrick, 2002; Savastano & Miller, 1998; R. S. Sutton & Barto, 1981), with the general suggestion that interval timing can arise simply through the competition between reinforced and nonreinforced behaviors across an interval and the memory for recent reinforcement, or with associational strength increasing as a function of time during a trial. In essence, an operant response is emitted not because the time of reinforcement is predicted, but rather because the operant response (or bout of operant responses: Kirkpatrick, 2002) is consistently more successful as the interval elapses (i.e., there is an increasing hazard function of reinforcement). Clockless models are attractive because they integrate seamlessly into existing information processing or learning theory without the need to conjure an independent timing mechanism or localize discrete brain regions for interval timing.
Learning to Time in the Peak-Time Procedure
Regardless of the type of clock (or lack thereof) used in timing models, each model must account for the observed data in peak-time procedures. Recent evidence now suggests that different learning processes may be responsible for the pre- and postpeak limbs of the peak-time curve. For example, Matell and Portugal (2007) found that rats trained to make a nose-poke response at an FI of 15 s showed a narrowing of the peak-time curve on extended test trials compared to brief initial test trials. This effect was asymmetrical, however, because rats stopped earlier on later trials than on earlier trials but showed no difference in start times between earlier and later trials. Kirkpatrick-Steger, Miller, Betti, and Wasserman (1996, Experiment 1) also showed a similar effect in pigeons, wherein birds were trained on 30-s FI discrete trials, followed by testing with 120-s peak trials. Responding increased rapidly toward the 30 s expected FI across all peak trials, but on the first peak trial, responding decreased only very gradually after 30 s, and peaks only narrowed by the end of the first six-trial block. A mostly symmetrical peak was noted on Days 25–30 and did not change substantially thereafter.
Even more dramatic effects were reported by Kaiser (2008), who trained rats to press a lever for food reinforcement on signaled FI 30-s trials. In the peak-time curve found when nonreinforced probe trials were introduced, averaged responding gradually changed from a flat curve to a more symmetrical Gaussian-like curve over 10 blocks of testing. This change in the peak-time curve was primarily caused by an initially shallow right limb of the curve that became progressively steeper over sessions. Of interest, this dramatic change in the shape of the peak-time curve was most marked when nonreinforced probe trials were introduced on 10% or 25% of the training trials but not when they were introduced on 50% of the training trials. If one assumed that the increased steepness of the right limb of the peak-time curve results from extinction of post-FI responding, this finding is puzzling, because a higher percentage of nonrewarded trials should lead to faster extinction.
One final example is found in a study of C3H mice trained to press a lever for milk reinforcement on a light-signaled FI 30-s schedule (Balci et al., 2009). Responding on non reinforced probe trials showed a consistent rise in responding over the first 30 s that changed little over 16 days of testing. On the other hand, mice showed no cessation of responding after 30 s on Day 1. Over successive test days, the right limb of the curve declined until it looked like the typical Gaussian peak-time curve by the final days of testing. Analysis of individual trials suggested that individual mice abruptly adopted stop behavior at different points during testing.
These findings suggest that the typical FI scallop seen in the left limb of the peak-time curve may develop early in FI training as a consequence of reward expectation. The right limb of the peak-time curve, however, may be controlled by extinction or learned inhibition of responding that occurs specifically during nonrewarded trials during the test phase. Such findings indicate some problems inherent in applying ideas of timing to real-world data, including the supposition that “starting” and “stopping” a clock have symmetrical effects on performance. They also emphasize the importance of associative learning in studies of timing and suggest that other learning processes might be involved in the study of behavioral timing. This is of particular interest given observations of cue competition effects in timing (e.g., Gaioni, 1982; Jennings, Bonardi, & Kirkpatrick, 2007; Jennings & Kirkpatrick, 2006; McMillan & Roberts, 2010). For example, McMillan and Roberts (2010) showed that pigeons could learn to time a compound stimulus with one stimulus element presented for 30 s and the other presented with 10 s remaining in the interval; pigeons demonstrated accurate fixed-interval responding on compound trials, as well as to either the “short” (10-s) or “long” (30-s) stimulus presented alone on probe trials. However, when pigeons were pretrained with the short (10 s) stimulus interval, the subjects failed to show accurate timing of a long (30 s) stimulus trained later in compound with the short stimulus. In this latter experiment, pigeons appeared to attend to only the most temporally proximal stimulus onset and failed to time a longer-duration stimulus despite pigeons in other conditions showing no such deficit with timing the 30-s stimulus. Whereas training both intervals together produces no “overshadowing” effect (McMillan & Roberts, 2010), pretraining with a short interval “blocked” learning of a longer interval when both were later compounded together. Although effects of cue competition between intervals have been somewhat mixed in the literature, initial findings suggest that processing of time may be subject to attention and competition for stimulus control, similar to competition frequently illustrated with low-level stimulus features such as shape and color.
We have also studied competition for stimulus control between temporal and nontemporal cue dimensions using the peak procedure (McMillan & Roberts, 2013a). Half of our pigeons were trained and tested with timed reinforcement occurring on a 60-s FI, whereas the other half were trained with pecks during a green stimulus reinforced on a 60-s FI and pecks to a red stimulus not reinforced after 60 s. After 20 sessions of training, these contingencies were reversed between groups. Regardless of order, pigeons showed typical peak-interval timing behavior while trained with 60-s FIs presented alone but showed profoundly flattened peak performance on identical 60-s FIs presented in context of other nonreinforced trials. Perhaps the most intriguing aspect of the overshadowing of temporal control by salient visual stimuli is that although interval time is not a valid predictor of whether food would be available, it was still valid for predicting when reward would be available. In a follow-up experiment we showed that pigeons would still time stimuli for a 50% chance at eventual reward, suggesting that time was important for efficient use of resources (i.e., reducing peck rate early in each trial, a time when food was not forthcoming). However, the mere presence of visually predicted nonrewarded trials led to a failure of temporal control over responding on rewarded trials. This suggests that time was treated similarly to visual identity as an attribute of each of the stimuli. Where time is often considered as a higher order cognitive capability of animals, processed separately and automatically in order to drive efficient responding, this research shows that time is nonetheless still processed as a component of stimuli and is subject to attention in the same manner as other stimulus dimensions.
One possible explanation for the effect of relative cue validity is that 60-s intervals were used in both reinforced and nonreinforced trials, creating a conflict between timed durations for predicting food that did not exist in the color dimension (i.e., green and red as 100% predictors of food vs. no food). This may be especially true because the competition effect was most pronounced on the right limb of the curves, consistent with a disruption in extinction learning; having very long S– trials may have limited the discriminability of S+ probe (extinction) trials relative to S– trials. We collected subsequent data presented next in order to rule out these possibilities.
Experiment 1: Relative Cue Validity Is Not Driven by Similar Duration
We trained four naïve adult White Carneaux pigeons (Columba livia) at the University of Western Ontario with S+ and S– stimuli appearing on alternate trials, followed by sessions with only S+ stimuli. All details of the procedure were identical to those previously used by McMillan and Roberts (2013a) for Group S+/S– → S+, except that the S– stimuli were presented for 15 s instead of 60 s.
For 20 sessions of 44 trials each, S+ and S– stimuli each appeared on 22 trials in random order. On both types of trials, the center key was lit white to start the trial, and pecks on the center key were recorded in 1-s bins. On S+ trials, the left sidekey also was lit with green light for two pigeons or with a white circle on a black background for the other two pigeons. The first peck made on the center key after a 60-s FI yielded 5 s of access to grain reinforcement. The center key and the S+ sidekey stayed on until either the first reinforced peck to the center key or 120 s had elapsed since the start of the trial. On S– trials, the center key appeared with the left sidekey lit red for the two birds that saw green as the S+ and lit with a white triangle for the two birds that saw circle as the S+. Pecking the center key was never reinforced on S– trials, and the keys turned off after 15 s. After a reinforced keypeck on S+ trials or the end of 15 s on S– trials, the chamber was darkened for an intertrial interval that varied randomly between 40 s and 80 s. After birds completed 10 sessions of training with S+ and S– stimuli, they were given 10 further sessions in which probe trials were introduced. Four nonrewarded probe trials were randomly interspersed among the 44 training trials. On probe trials, the S+ stimulus was presented for 120 s, and pecks were recorded throughout this period.
All birds showed increasing peck rates over the FI on S+ trials. By the third session of training and thereafter, responding on S– trials was negligible. Figure 2 shows relative response rates plotted over 120 s of S+ presentation on nonrewarded probe trials, compared with previous data collected by McMillan and Roberts (2013a). Particularly noticeable is that the right limb of curves for S+/S- training phases shows little decline in response rate past the FI (60 s), whereas the curve for pigeons without an S– present during training shows a clear decline in response rate. We have previously established that the effect of S+/S– training does not depend on whether it preceded or followed training with the S+ alone. Although most studies have pigeons responding on the timed stimulus, and here we train pigeons to respond on a center key in order to detach the response from the separate stimuli, the red and green sidekeys are well within the pigeons’ lateral vision, and McMillan and Roberts (2013a) have clearly demonstrated learning of an S+ condition with attention to a sidekey (see also Figure 1a of this article).
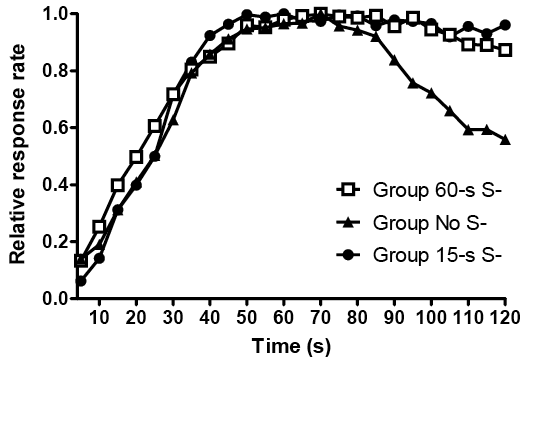
Figure 2. Peak-time curves generated by pigeons’ responding during the presence of a stimulus predicting FI 60-s reinforcement in the described experiment (Group 15-s S–), compared to responding by pigeons in Experiment 1 of McMillan and Roberts (2013a) with similar S+/S– training (Group 60-s S–) or only S+ training (Group No S–). All data taken during Sessions 11–20 across groups. The data have been relativized to a peak rate of 1.0 and plotted as a function of 5-s time bins.
These results are consistent with previous results shown by McMillan and Roberts (2013a) on a very similar procedure, and suggest that similar durations cannot account for the overshadowing of time by stimulus color on this task. Instead, relative cue validity (i.e., color as a cue for food vs. no food; time as cue for temporal location of food) alone determined the control of time over pigeons’ behavior on this task. Together with previous results in associative learning studies examining cue competition effects between intervals (e.g., Gaioni, 1982; Jennings et al., 2007; Jennings & Kirkpatrick, 2006; McMillan & Roberts, 2010), it is clear that timing is not automatic and instead that time is a cue dimension that competes with other cues for control over behavior. Further, even the control by time that exists in a typical peak procedure is the result of excitatory and inhibitory training. These results paint time as a discriminatory cue not divorced from other associational or operant processes, but rather very similar to the visual and auditory cue dimensions that make up the holistic stimuli from which time is derived.
Ordering Events in Time
Despite the usefulness of the peak-time procedure and temporal bisection task for studying timing from a general systems point of view, one problem with typical interval timing studies is their artificial nature; it is unlikely that animals in the wild frequently need to exactly reproduce an interval of time or compare two stimulus durations. Sometimes these kinds of tasks are explained in the context of monitoring foraging patch payoff or replenishment times, and although for some nectivorous animals this may be highly relevant (e.g., see Boisvert & Sherry, 2006; Henderson, Hurly, Bateson, & Healy, 2006; Toelch & Winter, 2013), this is not an ideal explanation for a common usage of time across species that could explain its ubiquity. Instead, it is more likely that interval timing is most useful for monitoring contiguity and the relationship of events across time. Although time is an important variable across a huge variety of behavioral tasks, which in turn helps explain its universal usefulness (Marshall & Kirkpatrick, 2015), one particularly relevant function is in determining order and duration across events. In this section we discuss two procedures that touch directly on these functions—serial pattern and time-place learning—in setting the stage for a related area of more recent study, midsession reversal.
Animals’ ability to represent serial order has been studied in a number of tasks, such as the delayed sequence-discrimination (DSD) procedure, where subjects are serially presented a number of stimuli in different sequences followed by a test stimulus, pecks in the presence of which are reinforced. Pigeons peck more on the test stimulus after the correct sequence than after incorrect sequences, showing successful discrimination on DSD tasks (e.g., Weisman, Duder, & von Konigslow, 1985; Weisman, Wasserman, Dodd, & Larew, 1980). Although timing has rarely been specifically invoked as part of the explanation in sequence learning procedures such as the DSD, solving these tasks could utilize an implicit temporal representation of the sequence. For instance, if presented with the sequence red–green–blue in successive order, knowing that red precedes blue is a temporal judgment; the subject must somehow represent when red happens relative to blue. Important to note, this judgment need not carry any interval information; whether red occurs 10 s or 100 s before blue in sequence is irrelevant to its order so long as the order is always red followed by green and then blue. Thus, if pigeons are capable of representing ordinality, they should be able to track both the identity of the sequence based on order of the stimuli across time (e.g., red–green–blue vs. green–red–blue) and the current position in the sequence relative to food (e.g., blue is proximal to food reward, green is less proximal, and red is least proximal). Other serial pattern procedures have explicitly studied the function of time within serial pattern learning, for example, the seminal work of Stephen Fountain (e.g., Fountain, Henne, & Hulse, 1984).
In their discussion of different types of timing, Carr and Wilkie (1997) described a relevant theoretical cognitive representation of time they referred to as ordinal timing. Ordinal timing was defined as the representation of events in a certain sequence over a period of time; for example, a bee may visit a particular sequence of flowers for the duration of each foraging bout (traplining). This concept is interesting because it is possible for ordinal and interval timing mechanisms to be separate representations of time with overlapping purposes of anticipating events using short-time temporal information (i.e., using either an ordinal sequence or interval timer to anticipate a particular future event). Most of the evidence Carr and Wilkie pointed to for this phenomenon was from field observation, with a single study in rats’ time-place learning as the lone laboratory example. Subsequent time-place experiments ruled out that rats used ordinal measurement to track food locations, and instead use either or both of interval and circadian timing to predict the locations of food (Crystal, 2009; Pizzo & Crystal, 2002, 2004, 2007). We also demonstrated that pigeons have difficulty learning a sequence of stimuli presented across a variable interval with one terminal reinforcer (McMillan & Roberts, 2013b). With extensive training, pigeons were able to demonstrate weakly rank-ordered responding to up to five stimuli in sequence, but only with explicit training wherein one sequence terminated in food and others did not. We suggested that this ability was likely derived from timing the interval across stimulus presentations, and perhaps rather than a discrete mechanism, ordinal “timing” results from the recruitment of more basic processes such as interval timing. Just as complex behavior organized across time can arise from simple timing processes (de Carvalho et al., 2016), so too may complex arrangements of stimuli be ordered using these processes; this capacity will be examined further in the next section.
When Happens Next? Time and Midsession Reversal
Recently, how behavior is organized across time has been extensively studied with a novel task arrangement dubbed midsession reversal (for a complete review, see Rayburn-Reeves & Cook, 2016), based nominally on serial reversal tasks. Where sequence discrimination tasks require attending to stimuli presented serially over time, reversal tasks involve flexibly altering behavior to static stimuli with changing task contingencies over time. In a prototypical serial reversal procedure, animals are trained with a simultaneous discrimination (e.g., reinforcement for responding to blue and not to yellow) with a reversal of contingencies occurring once the task is acquired (e.g., reinforcement for response to yellow and not to blue), with a reversal following each successive acquisition of the new discrimination (Mackintosh, McGonigle, Holgate, & Vanderver, 1968). With successive reversals, a variety of animals show improved speed to reacquisition relative to baseline, suggesting that behavioral flexibility is adaptively valuable (Shettleworth, 2010), and this phenomenon has been studied using many models of choice (e.g., Davis, Staddon, Machado, & Palmer, 1993).
The midsession reversal procedure makes only one small change to the serial reversal task: Instead of reversals occurring between sessions after meeting a criterion, reversals instead occur during each session. Generally, a subject is presented with two stimuli; responding to one is correct for the first half of trials, and responding to the other is correct on the second half of trials. As in the typical reversal procedure, the optimal strategy in the midsession reversal task is to respond based on the outcome of the last trial: If the response on the last trial was reinforced, then the animal should make the same response on the next trial, and if the response was nonreinforced then the subject should shift and respond to the other stimulus on the next trial (referred to as win/stay, lose/shift). However, pigeons (see Figure 3A) make a large number of anticipatory errors (i.e., responding to the second-correct stimulus before the reversal) and perseverative errors (i.e., responding to the first-correct stimulus after the reversal) in contrast to the performance by humans (Rayburn-Reeves, Molet, & Zentall, 2011) and rats (Rayburn-Reeves, Stagner, Kirk, & Zentall, 2013; but see McMillan, Kirk, & Roberts, 2014). These errors suggest that, rather than remembering the response and outcome from the previous trial to obtain optimal reinforcement, pigeons rely on an alternate strategy to predict the occurrence of the reversal.
Figure 3. (A; Upper Panel) Choice of the first-correct stimulus (S1) by pigeons in a simultaneous-choice midsession reversal procedure, and (B; Lower Panel) comparison of “go” responses to S1 and S2 in a successive-choice midsession reversal procedure. Data averaged across the last 25 sessions of training, at 80 trials per session. Vertical hatched lines indicate contingency reversal (after Trial 40). Data previously presented in McMillan et al. (2015).
There are only two obvious cognition-based explanations by which the pigeons could predict the reversal point. One strategy is to track the approximate number of trials (or reinforcers) until the change in contingencies (“The reversal occurs after 40 trials”). Alternatively, the pigeons could be tracking the interval time since the start of the session (“The reversal occurs after about 300 seconds”), taking advantage of the asymptotic speed at which they proceed through the session to predict the midpoint. In either of these cases, anticipatory and perseverative errors subsequently occur because the representations of number and time in animals are noisy estimates (and/or because of the slow shift in associative states across time; Machado & Guilhardi, 2000). Based on results of injecting large empty temporal gaps during sessions (Cook & Rosen, 2010) or altering the duration of intertrial intervals (McMillan & Roberts, 2012), it has been suggested that pigeons’ gradual switch behavior is exclusively governed by elapsed time. Delaying session onset has also been shown to disrupt performance (McMillan et al., 2015), suggesting that at least one interval used by pigeons is simply the duration starting from being placed in the operant chamber. Nontemporal endogenous cues, such as levels of satiety, have also been ruled out as potential switching factors (Cook & Rosen, 2010). This time-based explanation makes the midsession reversal procedure conceptually as well as procedurally similar to the free-operant psychophysical procedure (Stubbs, 1980).
This procedure has been performed with conditional reversals in matching-to-sample/oddity-from-sample discrimination (Cook & Rosen, 2010; Daniel, Cook, & Katz, 2015), simultaneous discrimination (e.g., McMillan & Roberts, 2012; Rayburn-Reeves et al., 2011), and sequential go/no-go discrimination (McMillan, Sturdy, & Spetch, 2015). If all three procedures are compared based on choice accuracy, behavior looks highly similar (see Figure 1 from Rayburn-Reeves & Cook, 2016) and can be robustly fit with a logistic function describing a gradual change in performance based on proximity to the reversal. Fundamentally, pigeons’ responding across these sessions appears to be probabilistic rather than categorical, despite that the reversal itself is from 100% to 0% probability of reward (or vice versa). Research has soundly demonstrated the robustness of the midsession reversal timing errors even with variable, difficult-to-predict reversal points (Rayburn-Reeves, Laude, & Zentall, 2013; Rayburn-Reeves & Zentall, 2013; Smith, Pattison, & Zentall, 2016). Even when actual switch points vary wildly across sessions, pigeons appear to form molar aggregate computations to anticipate the switch, and make only modest corrections based on a molecular “follow the reward” rule (Rayburn-Reeves, Laude, et al., 2013).
Subsequent research in our lab (McMillan et al., 2014) showed near-perfect maximization of reward in pigeons in a variable-trial midsession reversal procedure, where the key distinguishing manipulation was the presentation of stimuli as a visual-spatial discrimination; where prior tasks had most commonly presented red and green discriminative cues counterbalanced between sides across trials, we presented red always on one side and green always on the other. Pigeons’ performance was noticeably better than even similar results found by McMillan and Roberts (2012), and the data showed that at least one pigeon had abandoned timing in favor of only following local reinforcement rates. Individual differences were also noticed in strategy use, with some pigeons still not optimally following reward. This suggests that what was previously reported as a species difference on the midsession reversal task is likely due to individual differences and artifacts of memory tasks presented spatially in operant chambers. Some pigeons are capable of reward-following on a spatial reversal, which could be a result of spatially orienting to the left or right sidekey during the intertrial interval, essentially “cheating” the memory component of the procedure (McMillan et al., 2014; Rayburn-Reeves, Laude et al., 2013).
We also trained rats on a spatial-discrimination midsession reversal on a T-maze (McMillan et al., 2014); food was available on one side for the first 12 trials of a session and on the other side for the remaining 12 trials. We found that rats made similar anticipatory and perseverative errors as found with pigeons on a visual discrimination task, and in direct conflict with previous work examining midsession reversal with a spatial discrimination (Rayburn-Reeves, Laude, et al., 2013). That rats show good reversal performance on a spatial discrimination in the Skinner box (Please change to Rayburn-Reeves, Stagner, Kirk, & Zentall, 2013) but not in a T-maze (McMillan et al., 2014)—where the choice point is spatially distinct from the start position—corroborates the suggestion that animals are capable of following local reinforcement on the midsession reversal procedure by prospectively orienting during the delay between trials. Broadly, animals will use a win/stay-lose/shift strategy in midsession reversal when working memory load is light but will instead use interval timing when working memory load is heavy (i.e., when tasked to remember both the response and the consequence of the last trial over a 6-s delay).
The relative immaturity of the midsession reversal literature is most sorely felt in comparative research; other than some conflicted reports of human and rat behavior on the task, there is little to describe what species differences exist in midsession reversal, and what those differences might be based on (e.g., avian vs. mammalian; different foraging histories). Recently we have attempted to expand the procedure to black-capped chickadees. Whereas previous midsession reversal tasks have illustrated anticipatory and perseverative errors in brief, highly structured sessions, we sought to demonstrate temporally based switching in a task that might be more relevant to typical foraging. For this purpose we used six wild-caught black-capped chickadees in a pseudo-free-operant procedure, wherein subjects were maintained in operant chambers for several months and were free to initiate and complete trials throughout the course of each day. The Sturdy lab specializes in auditory go/no-go discrimination tasks with chickadees, and having previously demonstrated anticipation and perseveration on go/no-go tasks in pigeons (McMillan et al., 2015; see Figure 3B) we created an analog task using auditory stimuli (2 kHz and 4 kHz pure sinewave tones) for use with chickadees. Chickadees completed trials throughout the day, with responses to 2 kHz tones reinforced with food and responses to 4 kHz tones punished with a timeout; these contingencies reversed every 40 trials, creating trial blocks roughly equivalent to those in typical midsession reversal procedures. Because such procedures normally are not presented in such a cyclical fashion, we trained three of the six chickadees with a 5-min signal light preceding “Trial 1” of each block of trials in order to demarcate the start of a “session.” Results from individual chickadees are presented in Figure 4. None of the chickadees showed any indication of successful discrimination, let alone reversal; this was true regardless of whether the start of the “session” was signaled with a signal light or not. We have subsequently illustrated this failure with trial blocks of up to 240 trials (and a reversal at Trial 120: McMillan et al., in press). We subsequently showed that the chickadees were perfectly capable of learning the basic go/no-go discrimination, as well as to reverse their behavior; however, even those chickadees that learned a reversal task later failed to perform the reversal when returned to the midblock reversal task. It was not until chickadees were trained with midday reversals that they were capable of successfully reversing their behavior, and even in this case showed no tendency to anticipate.
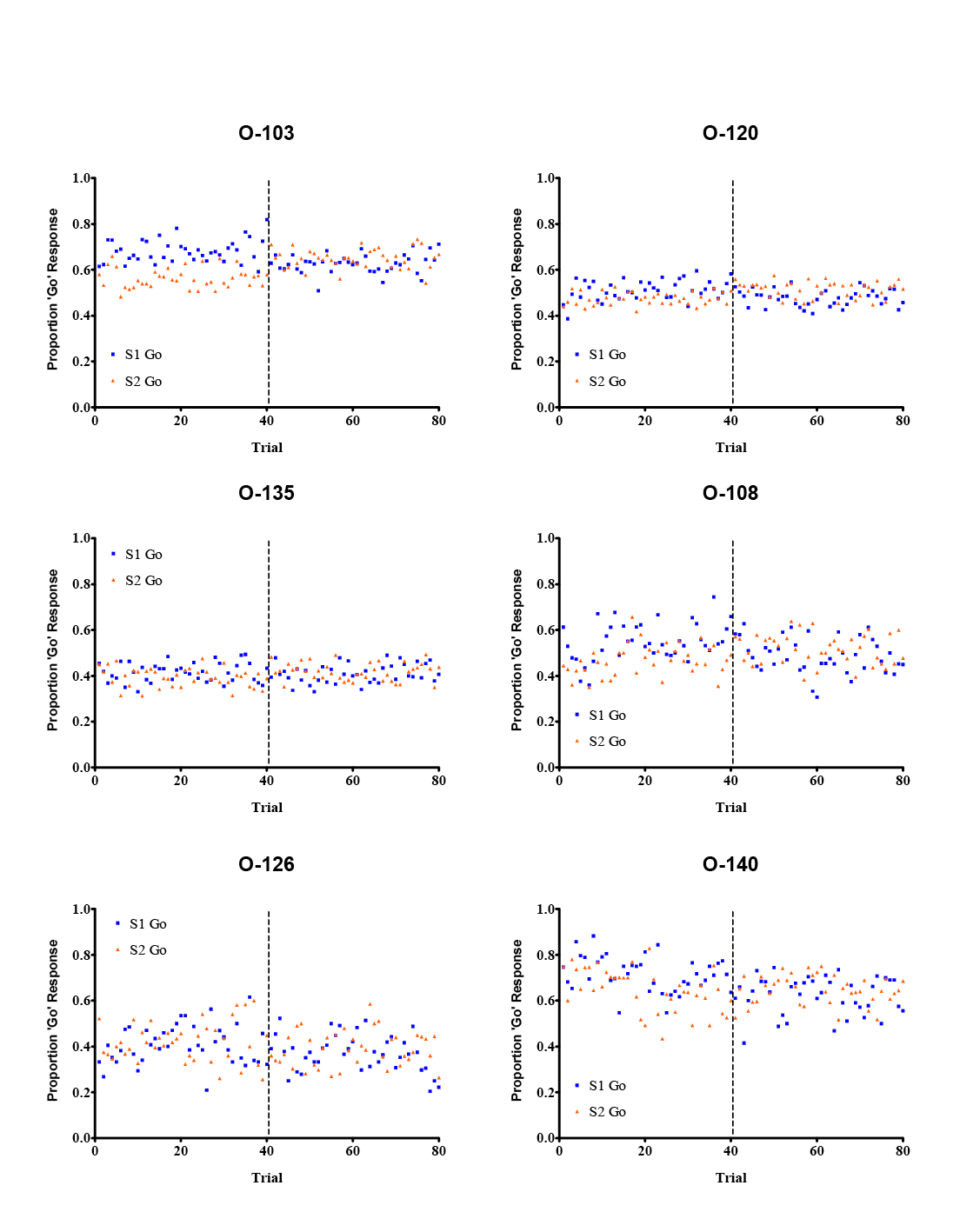
Figure 4. Go/no-go discrimination performance on a midsession reversal procedure in six black-capped chickadees: O-103, O-120, and O-135 were trained without a red cue light; O-108, O-126, and O-140 were trained with red cue light between sessions. Vertical hatched lines indicate contingency reversals after Trial 40.
Chickadees’ difficulty in learning a pseudo-midsession reversal task is difficult to resolve against previous data. The main difference between our procedure with chickadees and that used previously with pigeons and rats is in the temporal structure of a session. Pigeons and rats in previous midsession reversal research have been limited to single daily sessions of between 20 and 240 trials each: Session durations rarely exceed several minutes and are remarkably consistent within-subjects, making timing the typical duration between the onset of the session and the reversal straightforward. By contrast, chickadees’ trial blocks were marked by inconsistent time between trials and only one cue to distinguish different “sessions.” It was likely very difficult for chickadees to learn any particular timing rules, in contrast to the very specific rules that pigeons have been suggested to learn (e.g., “only respond to S2 after 3 min”: McMillan et al., 2015).
To study this phenomenon more closely, we trained four pigeons in a visual go/no-go task identical to that used by McMillan and colleagues (2015) except that the first-correct stimulus (S1+) for each session alternated across sessions (i.e., the S1+ for one session was the S2+ for the next, and vice versa). Importantly, this manipulation prevented pigeons from being able to memorize a single time-response pattern (e.g., “always wait 3 min to respond to green”) while otherwise maintaining all of the same features of a typical midsession reversal task (e.g., trial time and number, session time, reversal location). This was meant to determine whether black-capped chickadees’ lack of discrimination was particular to that species or procedural preparation, or rather if discrimination in midsession reversal hinges on having strict session temporal structure. In other words, we sought to bridge the results of McMillan et al. (2015), which had found successful discrimination and reversal performance on a go/no-go midsession reversal task in pigeons, with the failure to discriminate shown by chickadees on an otherwise-similar task (McMillan et al., in press).
Experiment 2: Pigeons Do Not Inhibit Incorrect Responses on a Go/No-Go Midsession Reversal Task Without Temporal Structure
On each trial for 80 trials per session, pigeons were presented with a blue-filled circle in the center of a gray background on the touchscreen. A single peck within the perimeter of the blue stimulus began the trial, leading immediately to the presentation of either a green- or red-filled circle on either the left or right side of the screen (with presentations of red vs. green and left vs. right randomized in blocks of four trials across the session). If the red or green stimulus was not pecked within 3 s of presentation, the stimulus was removed and was followed by a 3-s inter-trial interval (ITI), with the screen background still lit gray, followed by a new trial. On odd-numbered sessions, a peck to the red circle was correct for the first 40 trials and a peck to the green circle was correct for the latter 40 trials; these contingencies were reversed for even-numbered sessions. A single peck within the perimeter of the green or red circle led to the immediate removal of the stimulus: Pecking the currently correct stimulus was subsequently reinforced with 1-s access to food (measured from the time that the pigeon first tripped the photobeam in the hopper); if the pigeon pecked the currently incorrect stimulus, the screen was blackened for 10 s (time out) before the next trial. Either result was followed by a 3-s ITI, with the screen background lit gray, subsequently followed by a new trial. Subjects were run for 50 sessions.
Pigeons’ midsession reversal performance over the last 20 sessions is illustrated in Figure 5. Similar to the data observed in chickadees, and in contrast to previous results in pigeons on a go/no-go midsession reversal task (McMillan et al., 2015; also see Figure 3B), discrimination performance by pigeons on the current task was generally poor. Only one subject (#18) showed any appreciable separation between response rates on each stimulus across time; three of four subjects responded completely nondifferentially throughout sessions.
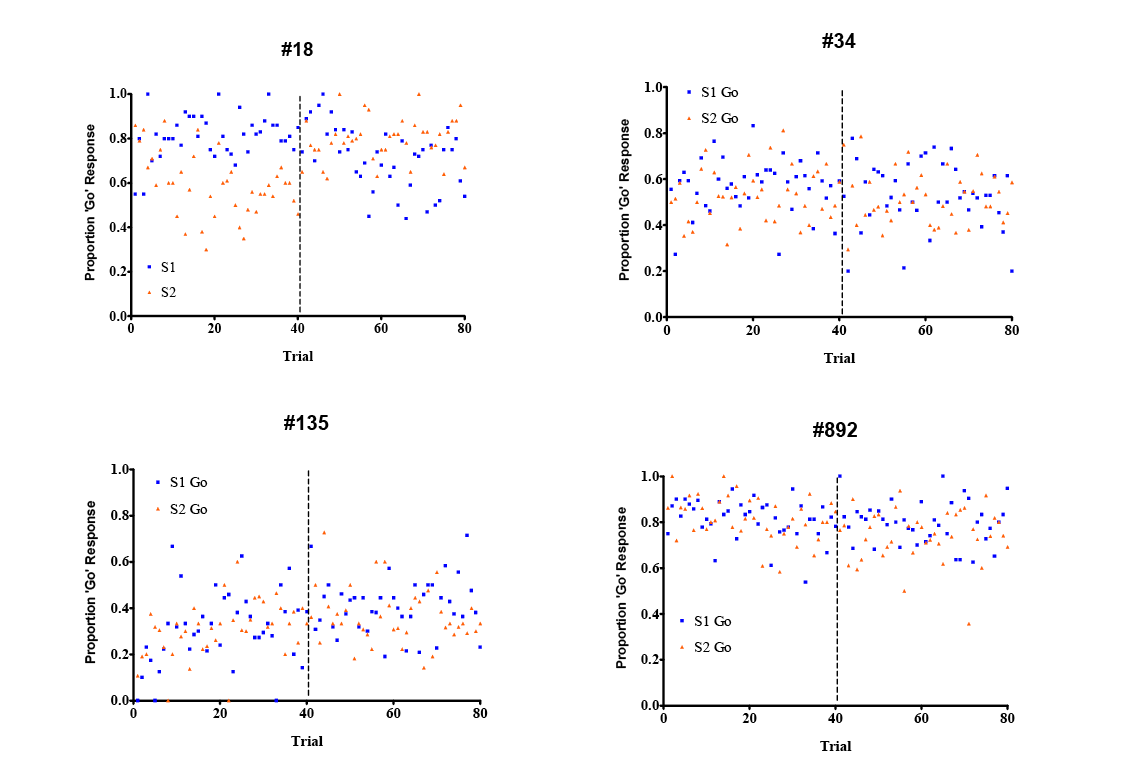
Figure 5. Go/no-go discrimination performance on a midsession reversal procedure in four pigeons. Vertical hatched lines indicate contingency reversals after Trial 40.
Attention to Temporal Structure in the Midsession Reversal Task
We have recently published similar data in pigeons on a simultaneous discrimination task (McMillan, Sturdy, Pisklak, & Spetch, 2016) in which the first-correct stimulus was alternated or randomized across sessions. Similar to results in a go/no-go tasks with pigeons and chickadees just described, pigeons on this procedure showed no control by time over behavior, and in this case began sessions at chance performance and only gradually improved prior to the reversal, and then shifted gradually after the reversal; there was no evidence of anticipation of the reversal under these conditions. It is thus clear that the basic structure of the midsession reversal task is fundamentally important for whether birds use time to predict the reversal.
Further, we have also replicated previous results of midsession reversal in humans (Rayburn-Reeves et al., 2011), but with both simultaneous and go/no-go task preparations and fixed versus alternating S1+s across blocks of trials (McMillan & Spetch, in prep) between four groups. With 10 blocks of 40-trial “sessions” and a reversal after Trial 20 each block, we found that several individuals illustrated errors qualitatively similar to pigeons’ with the same S1+ each block; contrarily, with alternating S1+s, humans, like pigeons, abandoned a timing-based approach, but they used only a “reward-following” rule in both cases (in contrast with pigeons, who simply show standard reversal functions; McMillan et al., 2016). We suggest that errors made on midsession reversal are qualitatively consistent across species, and that rats and humans are simply better at inhibiting erroneous time-based responding; further, animals (including humans) show no control by time in situations where time is either difficult to attach to simple “rules” across a session and/or when other strategies (such as postural cues during an ITI) are made dramatically more valid predictors of food.
Taken together, these results all paint a confusing picture of the role interval time plays in midsession reversal. In many versions of the task, time is a primary driver of pigeons’ behavior, even in cases where it results in many errors. In other procedures with only slight modifications, pigeons’ behavior shows little control by time, which subsequently results in few errors (McMillan et al., 2014; McMillan & Roberts, 2012) when there is an easy alternative strategy, or an enormous number of errors (McMillan et al., 2016; McMillan et al., in press) when there is not. The most consistent thread throughout these studies is that time “trades off,” competes, and/or integrates with other processes (including exogenous modulatory cues; see Rayburn-Reeves, Qadri, Brooks, Keller, & Cook, in press). Time rarely has total or zero control over behavior but instead is used based on its relative utility compared to other cues, similar to the results of McMillan and Roberts (2013a). The conflict between time and other processes does not seem to impact reaction times across the session (Rayburn-Reeves & Cook, 2016), which could suggest that these processes exist in a “horse race” to exert stimulus control over behavior, especially during the reversal-proximal intermediate phase of the session where time and reinforcement conflict maximally.
Conclusion: Timing and Attention
Timing has previously been suggested to be an automatic process (Roberts et al., 2000; J. E. Sutton & Roberts, 1998; Tse & Penney, 2006). Most theories of interval timing consider the clock as an internal neural mechanism, detached and independent from other learning processes. However, the work described in the present review suggests that the interval timing mechanism (a) fails to control behavior when placed in competition with more salient visual cues for reward versus nonreward, (b) can compromise with other serial learning processes to solve cognitively demanding ordinal or time-place learning tasks, and (c) competes with other decision-making processes in midsession reversal tasks based on how stimuli are presented. Overall, the use versus nonuse of interval time throughout these very different procedures is governed by relatively simple modifications of cue dimension and reward versus nonreward contingencies. Together, these results suggest that timing is much more affected by and integrated with other learning processes than commonly thought.
It is frequently difficult to disentangle attentional effects on timing behavior with actual changes to the clock described in various timing models. For example, dopaminergic agonists have previously been shown to produce peak-curve shifts and time estimates consistent with speeding up of the internal interval clock (and the opposite effects are observed with dopaminergic antagonists), whereas cholinergic drugs produce effects more consistent with changes to memory for time rather than processing of time (Meck, 1983, 1986). However, other evidence has questioned these explanations of dopaminergic effects on interval timing, suggesting that observed data may be driven by the attentional effects of dopamine rather than only adjustments in the internal clock (Santi, Weise, & Kuiper, 1995; Stanford & Santi, 1998). Consistent with these attentional interpretations of biases in duration estimates, in the human literature, predictable biases are introduced in timing when participants are required to perform any of a wide variety of nontemporal tasks while required to time an interval: In general, the less attention paid to time, the shorter the estimates of elapsed time (Block & Zakay, 1996; Brown, 1997, 2008). Participants are capable of attention sharing between concurrent timing and nontemporal processing, but systematically limiting attentional resources to timing produces “short”-biased estimates of time. This effect has also been shown in animals (Lejeune, Macar, & Zakay, 1999; J. E. Sutton & Roberts, 2002). These effects are sometimes interpreted as being caused by a switch (in the same language as scalar expectancy theory) that “leaks” accumulated pulses when interrupted, such as by being stopped and restarted; other models conjure an entirely separate attentional gate (Zakay & Block, 1995).
Rather than showing systematic biases in timing accuracy as is common in other studies of attention to time, the focus of the current review is on studies that involve subtle manipulations that affect the control exerted by time over behavior. For example, in the two novel experiments presented, pigeons opted to use salient visual cues that predicted reinforcement or local reinforcement rates under some arrangements of stimulus dimension and reinforcement contingencies, where in other conditions pigeons showed control by timing. These disruptions in temporal control could be due to attention shifts; for example, in considering scalar expectancy theory, attentional control could be attributable to the switch process, determining whether the organism times a particular interval. However, this does not specifically explain why a pigeon would fail to accurately time a 60-s interval when presented with nonreinforced intervals, especially if it has previously been subject to good control by time on 60-s reinforced intervals presented alone. Many timing theories also assume that intervals are timed based on the onset of a particular stimulus with a discrete reinforcer ending the interval, an assumption that is challenged both by successful timing of multiple stimuli presented in sequence and by timing an interval from the onset of the session rather than between stimuli or between reinforcers, as shown in the midsession reversal procedure. Just as motivational properties of timing performance are useful for discriminating between timing theories (see Daniels & Sanabria, 2016), so too does how well a theory integrates time with other stimulus control processes.
A central limitation of most traditional theories of timing is that they are only prospective timing models: They only speak to that timing that occurs with the onset of a stimulus in preparation for delivery of reinforcement, and not to retrospective situations such as incidental timing (e.g., as shown in pigeons by Roberts et al., 2000). The inflexibility of the clock mechanism in these models is hardly coherent with the human experience of timing: If you were asked how long you had been reading this paragraph or this review, you could produce ballpark estimates without having any discrete cue with which to “start a clock.” Ought the timing mechanism in nonhuman animals be radically different, simply because this was a distinction made 40 years ago (see Hicks, Miller, & Kinsbourne, 1976)? Midsession reversal also holds special interest as an exception to the typical rule in interval timing models that the clock is synchronized to individual reinforcer deliveries (but see Bizo & White, 1994); as compared to typical timing experiments, where animals time between reinforcers, in midsession reversal they time across them. In general, timing seems both more flexible and more fragile than models of timing frequently account for.
Clockless models that consider timing an emergent property of information processing (Ornstein, 1969) or behavior (Dragoi et al., 2003; Kirkpatrick, 2002; Machado, 1997) are immediately amenable to attentional effects on timing and temporal control, and more conventional models of timing would benefit from being more closely integrated with learning models to explain effects like those observed in the present review. Examples of attempts for integrative timing theories include the temporal delay hypothesis (R. S. Sutton & Barto, 1990), the learning-to-time model (Machado, 1997), and the behavioral economic model (Jozefowiez, Staddon, & Cerutti, 2009). These theories generally describe how subjects learn about time and its relationship to reinforcement. Crucially, each theory commonly predicts that particular behaviors and responses become more closely associated with food as the interval elapses, essentially making the animal’s own behavior the clock rather than necessitating separate pacemakers. In the general case, these theories of timing allow for direct integration of timing with attentional and learning processes, by virtue of timing being treated as an intrinsic property of behavior rather than as an independent neural mechanism.
Traditional models of time (notably scalar timing theory) and strictly neural-based timers (such as striatal beat-frequency) are not necessarily incompatible with the current results. Attentional processes are capable of acting on different aspects of these models, though they are not always well described; for example, the striatal beat-frequency model involves frontal-striatal neural pathways (Matell & Meck, 2000, 2004) the implicated roles of which also include attention, suggesting one possible avenue for integrating these models. Important to note, the results summarized here cannot rule out that subjects failed to time. In any of the negative cases, pigeons could have accurately timed the contingent interval but not shown stimulus control by timing. Lejeune and Wearden (1991) compared interval timing across a variety of species and found that certain species showed greater timing accuracy than others; however, the authors concluded that differences in observed timing ability were in large part due to differences in tasks (e.g., a fish tank is quite different from a rat operant chamber) and the ability to inhibit nontimed behavior (e.g., cats are better able to inhibit random responding than are pigeons), rather than species differences in sensitivity to time. In the same manner, the present results could be compatible with the interpretation that pigeons timed the contingent intervals but that time failed to control behavior in competition with other nontemporal processes. Behavioral control by time appears to be modulated by relative cue validity, the presence of more proximal predictors for reward, and attentional or working memory load for other processes.
In sum, the results reported in this review show differences in how animals use timing in a variety of procedures with simple manipulations of stimulus and reward presentation. These results are inconsistent with interval timing being purely an automatic contributor to behavior, mechanistically processed internally and not affected by external factors. Instead, time should be considered an important element of the complex stimulus compounds that comprise all environments, as well as a very important component of standard learning processes. Behavior- and associational-based theories of timing may be better situated to explain many of these results, but other models of timing should be integrated with associative approaches to better model the links between learning, timing, and attention.
References
Antle, M. C., & Silver, R. (2009). Neural basis of timing and anticipatory behaviors. European Journal of Neuroscience, 30, 1643–1649. doi:10.1111/j.1460-9568.2009.06959.x
Arcediano, F. & Miller, R. R. (2002). Some constraints for models of timing: A temporal coding hypothesis perspective. Learning & Motivation, 33, 105–123. doi:10.1006/lmot.2001.1102
Balci, F. (2015). Interval timing behavior: Comparative and integrative approaches. International Journal of Comparative Psychology, 28, 1–6.
Balci, F., Gallistel, C. R., Allen, B. D., Frank, K. M., Gibson, J. M., & Brunner, D. (2009). Acquisition of peak responding: What is learned? Behavioural Processes, 80, 67–75. doi:10.1016/j.beproc.2008.09.010
Bizo, L. A., & White, K. G. (1994). Pacemaker rate in the behavioral theory of timing. Journal of Experimental Psychology, 20, 308–321. doi:10.1037/0097-7403.20.3.308
Block, R. A., & Zakay, D. (1996). Models of psychological time revisited. In H. Helfrich (Ed.), Time and mind (pp. 171–195). Bern, Switzerland: Hogrefe & Huber.
Boisvert, M. J., & Sherry, D. F. (2006). Interval timing by an invertebrate, the bumble bee Bombus impatiens. Current Biology, 16, 1636–1640. doi:10.1016/j.cub.2006.06.064
Brown, S. W. (1997). Attentional resources in timing: Interference effects in concurrent temporal and nontemporal working memory tasks. Perception & Psychophysics, 59, 1118–1140. doi:10.3758/BF03205526
Brown, S. W. (2008). Time and attention: Review of the literature. In S. Grondin (Ed.), Psychology of time (pp. 111–138). Bingley, UK: Emerald Group.
Buhusi, C. V., & Meck, W. H. (2005). What makes us tick? Functional and neural mechanisms of interval timing. Nature Reviews Neuroscience, 6, 755. doi:10.1038/nrn1764
Carr, J. A. R., & Wilkie, D. M. (1997). Ordinal, phase, and interval timing. In C. M. Bradshaw & E. Szabadi (Eds.), Time and behaviour: Psychological and neurobehavioural analyses (pp. 265–327). Amsterdam, the Netherlands: North-Holland/Elsevier. doi:10.1016/S0166-4115(97)80059-3
Catania, A. C. (1970). Reinforcement schedules and psychophysical judgments: A study of some temporal properties of behavior. In W. N. Schoenfeld (Ed.), The theory of reinforcement schedules (pp. 1–42). New York, NY: Appleton-Century-Crofts.
Cheng, K., & Westwood, R. (1993). Analysis of single trials in pigeons’ timing performance. Journal of Experimental Psychology: Animal Behavior Processes, 19, 56–67. doi:10.1037/0097-7403.19.1.56
Church, R. M., & Broadbent, H. A. (1990). Alternative representations of time, number, and rate. Cognition, 37, 55–81. doi:10.1016/0010-0277(90)90018-F
Church, R. M., & Deluty, M. Z. (1977). Bisection of temporal intervals. Journal of Experimental Psychology: Animal Behavior Processes, 3, 216–228. doi:10.1037/0097-7403.3.3.216
Cook, R. G., & Rosen, H. (2010). Temporal control of internal states in pigeons. Psychonomic Bulletin & Review, 17, 915–922.
Crystal, J. D. (2009). Theoretical and conceptual issues in time-place discrimination. European Journal of Neuroscience, 30, 1756–1766. doi:10.1111/j.1460-9568.2009.06968.x
Crystal, J. D. (2012). Sensitivity to time: Implications for the representation of time. In T. R. Zentall & E. A. Wasserman (Eds.), Oxford handbook of comparative cognition (pp. 434–450). New York, NY: Oxford University Press.
Crystal, J. D. (2015). Rats time long intervals: Evidence from several cases. International Journal of Comparative Psychology, 28, 1–12.
Daniel, T. A., Cook, R. G., & Katz, J. S. (2015). Temporal dynamics of task switching and abstract-concept learning in pigeons. Frontiers in Psychology, 6, 1334. doi:10.3389/fpsyg.2015.01334
Daniels, C. W., & Sanabria, F. (2016). Interval timing under a behavioral microscope: Dissociating motivation and timing processes in fixed-interval performance. Learning & Behavior, 29–48. doi:10.3758/s13420-016-0234-1
Davis, D. G. S., Staddon, J. E. R., Machado, A., & Palmer, R. G. (1993). The process of recurrent choice. Psychological Review, 100, 320–341. doi:10.1037/0033-295X.100.2.320
de Carvalho, M. P., Machado, A., & Vasconcelos, M. (2016). Animal timing: A synthetic approach. Animal Cognition, 19, 707–732. doi:10.1007/s10071-016-0977-2
Dragoi, V., Staddon, J. E. R., Palmer, R. G., & Buhusi, C. V. (2003). Interval timing as an emergent learning property. Psychological Review, 110, 126–144. doi:10.1037/0033-295X.110.1.126
Fountain, S. B., Henne, D. R., & Hulse, S. H. (1984). Phrasing cues and hierarchical organization in serial pattern learning by rats. Journal of Experimental Psychology: Animal Behavior Processes, 10, 30–45. doi:10.1037/0097-7403.10.1.30
Gaioni, S. J. (1982). Blocking and nonsimultaneous compounds: Comparison of responding during compound conditioning and testing. Pavlovian Journal of Biological Science, 17, 16–29. doi:10.1007/BF03003472
Galtress, T., & Kirkpatrick, K. (2009). Reward value effects on timing in the peak procedure. Learning and Motivation, 40, 109–131. doi:10.1016/j.lmot.2008.05.004
Galtress, T., & Kirkpatrick, K. (2010). Reward magnitude effects on temporal discrimination. Learning and Motivation, 41, 108–124. doi:10.1016/j.lmot.2010.01.002
Gibbon, J. (1977). Scalar expectancy theory and Weber’s law in animal timing. Psychological Review, 84, 279–325. doi:10.1037/0033-295X.84.3.279
Gibbon, J., & Church, R. M. (1984). Sources of variance in an information processing theory of timing. In H. L. Roitblat, T. G. Bever, & H. S. Terrace (Eds.), Animal cognition (pp. 465–488). Hillsdale, NJ: Erlbaum.
Gibbon, J., & Church, R. M. (1990). Representation of time. Cognition, 37, 23–54. doi:10.1016/0010-0277(90)90017-E
Gibbon, J., Church, R. M., & Meck, W. H. (1984). Scalar timing in memory. In J. Gibbon & L. Allan (Eds.), Timing and time perception (Annals of the New York Academy of Sciences) (Vol. 423, pp. 52–77). New York, NY: New York Academy of Sciences. doi:10.1111/j.1749-6632.1984.tb23417.x
Grossberg, S., & Schmajuk, N. A. (1989). Neural dynamics of adaptive timing and temporal discrimination during associative learning. Neural Networks, 2, 79–102. doi:10.1016/0893-6080(89)90026-9
Henderson, J., Hurly, A. T., Bateson, M., & Healy, S. D. (2006). Timing in free-living rufous hummingbirds, Selasphorus rufus. Current Biology, 16, 512–515. doi:10.1016/j.cub.2006.01.054
Hicks, R. E., Miller, G. W., & Kinsbourne, M. (1976). Prospective and retrospective judgments of time as a function of amount of information processed. The American Journal of Psychology, 89, 719–730. doi:10.2307/1421469
Jennings, D. J., Bonardi, C., & Kirkpatrick, K. (2007). Overshadowing and stimulus duration. Journal of Experimental Psychology: Animal Behavior Processes, 33, 464–475. doi:10.1037/0097-7403.33.4.464
Jennings, D. J., & Kirkpatrick, K. (2006). Interval duration effects on blocking in appetitive conditioning. Behavioural Processes, 71, 318–329. doi:10.1016/j.beproc.2005.11.007
Jozefowiez, J., Staddon, J. E. R., & Cerutti, D. T. (2009). The behavioral economics of choice and interval timing. Psychological Review, 116, 519–539. doi:10.1037/a0016171
Kaiser, D. H. (2008). The proportion of fixed interval trials to probe trials affects acquisition of the peak procedure fixed interval timing task. Behavioural Processes, 77, 100–108. doi:10.1016/j.beproc.2007.06.009
Killeen, P. R., & Fetterman, J. G. (1988). A behavioral theory of timing. Psychological Review, 95, 274–295. doi:10.1037/0033-295X.95.2.274
Kirkpatrick, K. (2002). Packet theory of conditioning and timing. Behavioural Processes, 57, 89–106. doi:10.1016/S0376-6357(02)00007-4
Kirkpatrick-Steger, K., Miller, S. S., Betti, C. A., & Wasserman, E. A. (1996). Cyclic responding by pigeons on the peak timing procedure. Journal of Experimental Psychology: Animal Behavior Processes, 22, 447–460. doi:10.1037/0097-7403.22.4.447
Lejeune, H., Cornet, S., Ferreira, M.A., & Wearden, J.H. (1998). How do Mongolian gerbils (Meriones unguiculatus) pass the time? Adjunctive behavior during temporal differentiation in gerbils. Journal of Experimental Psychology: Animal Behavior Processes, 24, 325–334. doi:10.1037/0097-7403.24.3.352
Lejeune, H., Macar, F., & Zakay, D. (1999). Attention and timing: Dual task performance in pigeons. Behavioral Processes, 44, 127–145. doi:10.1016/S0376-6357(98)00045-X
Lejeune, H., & Wearden, J. H. (1991). The comparative psychology of fixed-interval responding: Some quantitative analyses. Learning and Motivation, 22, 84–111. doi:10.1016/0023-9690(91)90018-4
Ludvig, E. A., Balci, F., & Spetch, M. L. (2011). Reward magnitude and timing in pigeons. Behavioural Processes, 86, 359–363. doi:10.1016/j.beproc.2011.01.003
Macar, F., & Vidal, F. (2009). Timing processes: An outline of behavioural and neural indices not systematically considered in timing models. Canadian Journal of Experimental Psychology, 63, 227–239. doi:10.1037/a0014457
Machado, A. (1997). Learning the temporal dynamics of behavior. Psychological Review, 104, 241–265. doi:10.1037/0033-295X.104.2.241
Machado, A., & Guilhardi, P. (2000). Shifts in the psychometric function and their implications for models of timing. Journal of the Experimental Analysis of Behavior, 74, 25–54. doi:10.1901/jeab.2000.74-25
Mackintosh, N. J., McGonigle, B., Holgate, V., & Vanderver, V. (1968). Factors underlying improvement in serial reversal learning. Canadian Journal of Psychology, 22, 85–95.
Marshall, A. T., & Kirkpatrick, K. (2015). Everywhere and everything: The power and ubiquity of time. International Journal of Comparative Psychology, 28, 1–29.
Matell, M. S., & Meck, W. H. (2000). Neuropsychological mechanisms of interval timing behavior. BioEssays, 22, 94–103. doi:10.1002/(SICI)1521-1878(200001)22:1<94::AID-BIES14>3.0.CO;2-E
Matell, M. S., & Meck, W. H. (2004). Cortico-striatal circuits and interval timing: Coincidence detection of oscillatory processes. Cognitive Brain Research, 21, 139–170.
Matell, M. S., & Portugal, G. S. (2007). Impulsive responding on the peak-interval procedure. Behavioural Processes, 74, 198–208. doi:10.1016/j.cogbrainres.2004.06.012
Matthews, W. J., & Meck, W. H. (2016). Temporal cognition: Connecting subjective time to perception, attention, and memory. Psychological Bulletin, 142, 865–907. doi:10.1037/bul0000045
McMillan, N., Hahn, A. H., Congdon, J. V., Campbell, K. A., Hoang, J., Scully, E. N., Spetch, M. L., & Sturdy, C. B. (in press). Chickadees discriminate contingency reversals based on performance criterion, but not time or number. Animal Cognition.
McMillan, N., Kirk, C. R., & Roberts, W. A. (2014). Pigeon (Columba livia) and rat (Rattus norvegicus) performance in the midsession reversal procedure depends upon cue dimensionality. Journal of Comparative Psychology, 128, 357–366. doi:10.1037/a0036562
McMillan, N., & Roberts, W. A. (2010). The effects of cue competition on timing in pigeons. Behavioural Processes, 84, 581–590. doi:10.1016/j.beproc.2010.02.018
McMillan, N., & Roberts, W. A. (2012). Pigeons make errors as a result of interval timing in a visual, but not a visual-spatial, midsession reversal task. Journal of Experimental Psychology: Animal Behavior Processes, 38, 440–445. doi:10.1037/a0030192
McMillan, N., & Roberts, W. A. (2013a). Interval timing under variations in the relative validity of temporal cues. Journal of Experimental Psychology: Animal Behavior Processes, 39, 334–341. doi:10.1037/a0032470
McMillan, N., & Roberts, W. A. (2013b). Pigeons rank-order responses to temporally sequential stimuli. Learning & Behavior, 41, 309–318. doi:10.3758/s13420-013-0106-x
McMillan, N., & Spetch, M. L. (submitted). Humans, like pigeons, anticipate a midsession reversal with fixed but not alternating contingency orders.
McMillan, N., Sturdy, C. B., Pisklak, J. M., & Spetch, M. L. (2016). Pigeons perform poorly on a midsession reversal task without rigid temporal regularity. Animal Cognition, 19, 855–859. doi:10.1007/s10071-016-0962-9
McMillan, N., Sturdy, C. B., & Spetch, M. L. (2015). When is a choice not a choice? Pigeons fail to inhibit incorrect responses on a go/no-go midsession reversal task. Journal of Experimental Psychology: Animal Learning and Cognition, 41, 255–265. doi:10.1037/xan0000058
Meck, W. H. (1983). Selective adjustments of the speed of the internal clock and memory processes, Journal of Experimental Psychology: Animal Behavior Processes, 9, 171–201. doi:10.1037/0097-7403.9.2.171
Meck, W. H. (1984). Attentional bias between modalities: Effect on the interval clock, memory, and decision stages used in animal time discrimination. In J. Gibbon & L. G. Allan (Eds.), Timing and time perception (pp. 528–541). New York: New York Academy of the Sciences. doi:10.1111/j.1749-6632.1984.tb23457.x
Meck, W. H. (1986). Affinity for the dopamine D2 receptor predicts neuroleptic potency in decreasing the speed of an internal clock. Pharmacological Biochemistry and Behavior, 25, 1185–1189. doi:10.1016/0091-3057(86)90109-7
Merchant, H., Harrington, D. L., & Meck, W. H. (2013). Neural basis of the perception and estimation of time. Annual Review of Neuroscience, 36, 313–336. doi:10.1146/annurev-neuro-062012-170349
Miall, R. C. (1989). The storage of time intervals using oscillating neurons. Neural Computation, 1, 359–371. doi:10.1162/neco.1989.1.3.359
Miki, A., & Santi, A. (2005). The perception of empty and filled time intervals by pigeons. Quarterly Journal of Experimental Psychology, 58, 31–45. doi:10.1080/0272499044000032
Ornstein, R. E. (1969). On the experience of time. New York, NY: Penguin.
Pizzo, M. J., & Crystal, J. D. (2002). Representation of time in time-place learning. Animal Learning & Behavior, 30, 387–393. doi:10.3758/BF03195963
Pizzo, M. J., & Crystal, J. D. (2004). Time-place learning in the eight-arm radial maze. Learning & Behavior, 32, 240–255. doi:10.3758/BF03196025
Pizzo, M. J., & Crystal, J. D. (2007). Temporal discrimination of alternate days in rats. Learning & Behavior, 35, 163–168. doi:10.3758/BF03193051
Rayburn-Reeves, R. M., & Cook, R. G. (2016). The organization of behavior over time: Insights from mid-session reversal. Comparative Cognition & Behavior Reviews, 11, 103–125. doi:10.3819/ccbr.2016.110006
Rayburn-Reeves, R. M., Laude, J. R., & Zentall, T. R. (2013). Pigeons show near-optimal win-stay/lose-shift performance on a simultaneous-discrimination, midsession reversal task with short intertrial intervals. Behavioural Processes, 92, 65–70. doi:10.1016/j.beproc.2012.10.011
Rayburn-Reeves, R. M., Molet, M., & Zentall, T. R. (2011). Simultaneous discrimination reversal learning in pigeons and humans: Anticipatory and perseverative errors. Learning & Behavior, 39, 125–137. doi:10.3758/s13420-010-0011-5
Rayburn-Reeves, R. M., Qadri, M. A. J., Brooks, D. I., Keller, A. M., & Cook, R. G. (2016). Dynamic cue use in pigeon mid-session reversal. Behavioural Processes, 53–63. doi:10.1016/j.beproc.2016.09.002
Rayburn-Reeves, R. M., Stagner, J. P., Kirk, C. R., & Zentall, T. R. (2013). Reversal learning in rats (Rattus norvegicus) and pigeons (Columba livia): Qualitative differences in behavioral flexibility. Journal of Comparative Psychology, 127, 202–211. doi:10.1037/a0026311
Richelle, M., & Lejeune, H. (Eds.). (1980). Time in animal behavior. Oxford, UK: Pergamon. doi:10.1016/B978-0-08-025489-0.50002-8
Roberts, S. (1981). Isolation of an internal clock. Journal of Experimental Psychology: Animal Behavior Processes, 7, 242–268. doi:10.1037/0097-7403.7.3.242
Roberts, W. A., Cheng, K., & Cohen, J. S. (1989). Timing light and tone signals in pigeons. Journal of Experimental Psychology: Animal Behavior Processes, 15, 23–35. doi:10.1037/0097-7403.15.1.23
Roberts, W. A., Coughlin, R., & Roberts, S. (2000). Pigeons flexibly time or count on cue. Psychological Science, 11, 218–222. doi:10.1111/1467-9280.00244
Roberts, W. A., & Grant, D. S. (1974). Short-term memory in the pigeon with presentation precisely controlled. Learning and Motivation, 5, 393–408. doi:10.1016/0023-9690(74)90020-4
Roberts, W. A., & Grant, D. S. (1976). Studies of short-term memory in the pigeon using the delayed matching-to-sample procedure. In D. L. Medin, W. A. Roberts, & R. T. Davis (Eds.), Processes of animal memory. Hillsdale, NJ: Erlbaum.
Roberts, W. A., & Grant, D. S. (1978). Interaction of sample and comparison stimuli in delayed matching to sample with the pigeon. Journal of Experimental Psychology: Animal Behavior Processes, 4, 68–82. doi:10.1037/0097-7403.4.1.68
Santi, A., Keough, D., Gagne, S., & Van Rooyen, P. (2007). Differential effects of empty and filled intervals on duration estimation by pigeons: Test of an attention-sharing explanation. Behavioural Processes, 74, 176–186. doi:10.1016/j.beproc.2006.08.008
Santi, A., Miki, A., Hornyak, S., & Eidse, J. (2005). The perception of filled and empty time intervals by rats. Learning & Motivation, 34, 282–302. doi:10.1016/S0023-9690(03)00021-3
Santi, A., Weise, L., & Kuiper, D. (1995). Amphetamine and memory for event duration in rats and pigeons: Disruption of attention to temporal samples rather than changes in the speed of the internal clock. Psychobiology, 23, 224–232. doi:10.3758/BF03332026
Savastano, H. I., & Miller, R. R. (1998). Time as content in Pavlovian conditioning. Behavioural Processes, 44, 147–162. doi:10.1016/S0376-6357(98)00046-1
Shettleworth, S. J. (2010). Cognition, evolution, and behavior (2nd ed.). New York, NY: Oxford University Press.
Smith, A. P., Pattison, K. F., & Zentall, T. R. (2016). Rats’ midsession reversal performance: The nature of the response. Learning & Behavior, 44, 49–58. doi:10.3758/s13420-015-0189-7
Staddon, J. E. R., & Higa, J. J. (1999). Time and memory: Towards a pacemaker-free theory of interval timing. Journal of the Experimental Analysis of Behavior, 71, 215–251. doi:10.1901/jeab.1999.71-215
Stanford, L., & Santi, A. (1998). The dopamine D2 agonist quinpirole disrupts attention to temporal signals without selectively altering the speed of the internal clock. Psychobiology, 26, 258–266. doi:10.3758/BF03330614
Sutton, J. E., & Roberts, W. A. (1998). Do pigeons show incidental timing? Some experiments and a hierarchical framework for the study of attention in animal cognition. Behavioural Processes, 44, 263–275. doi:10.1016/S0376-6357(98)00053-9
Sutton, J. E., & Roberts, W. A. (2002). The effect of nontemporal information processing on time estimation in pigeons. Learning & Motivation, 33, 124–140. doi:10.1006/lmot.2001.1103
Sutton, R. S., & Barto, A. G. (1990). Time derivative models of Pavlovian reinforcement. In M. R. Gabriel & J. W. Moore (Eds.), Learning and computational neuroscience: Foundations of adaptive networks (pp. 497–537). Cambridge, MA: MIT Press.
Stubbs, D. A. (1980). Temporal discrimination and a free-operant psychophysical procedure. Journal of the Experimental Analysis of Behavior, 33, 167–185. doi:10.1901/jeab.1980.33-167
Toelch, U., & Winter, Y. (2013). Interval timing behavior in Pallas’s long-tongued bat (Glossophaga soricina). Journal of Comparative Psychology, 127, 445–452. doi:10.1037/a0032528
Tse, C-Y., & Penney, T. B. (2006). Preattentive timing of empty intervals is from marker offset to onset. Psychophysiology, 43, 172–179. doi:10.1111/j.1469-8986.2006.389.x
Wearden, J. (2016). The psychology of time perception. London, UK: Palgrave McMillan. doi:10.1057/978-1-137-40883-9
Weisman, R. G., Duder, C., & von Konigslow, R. (1985). Representation and retention of three-event sequences in pigeons. Learning and Motivation, 16, 239–258. doi:10.1016/0023-9690(85)90014-1
Weisman, R. G., Wasserman, E. A., Dodd, P. W. D., & Larew, M. B. (1980). Representation and retention of two-event sequences in pigeons. Journal of Experimental Psychology: Animal Behavior Processes, 6, 312–325. doi:10.1037/0097-7403.6.4.312
Wilkie, D. M. (1987). Stimulus intensity affects pigeons’ timing behavior: Implications for an internal clock model. Animal Learning & Behavior, 15, 35–39. doi:10.3758/BF03204901
Wynne, C. D. L., & Staddon, J. E. R. (1988). Typical delay determines waiting time on periodic-food schedules: Static and dynamic tests. Journal of the Experimental Analysis of Behavior, 50, 197–210. doi:10.1901/jeab.1988.50-197
Zakay, D., & Block, R. A. (1995). An attentional gate model of prospective time estimation. In M. Richelle, V. DeKeyser, G. d’Ydewalle, & A. Vandierendock (Eds.), Time and the dynamic control of behavior (pp. 167–178). Liège, Belgium: Université de Liège, P.A.I.
